The arguments are generally next to each other.
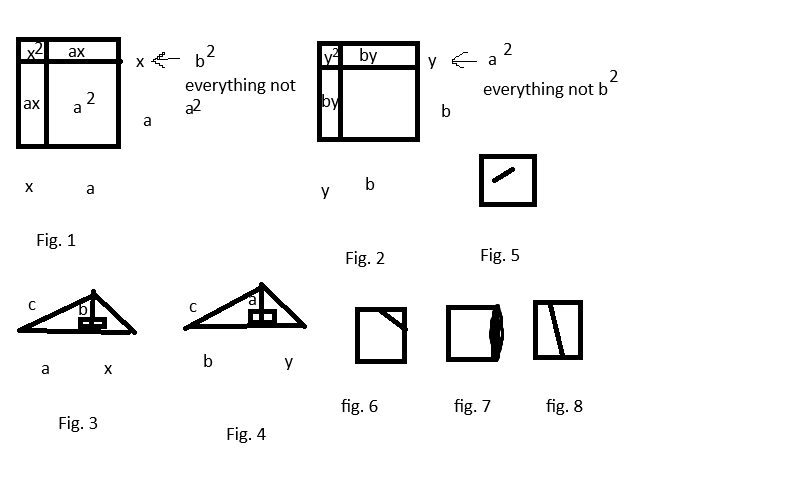
In fig. 1, x is defined so that ax+ax+x2 = b2, and in fig. 2 y is defined so that by+by+y2=a2.
Fig. 1 and Fig. 2 have the same area a2+b2, and they are square, so they have the same edges in each and together. a2+02=c2 and 02+02=02 are trivial. The edges are all a+x and b+y.
Fig. 3 and 4 suggest c=a+x and c=b+y, but you can ignore this.
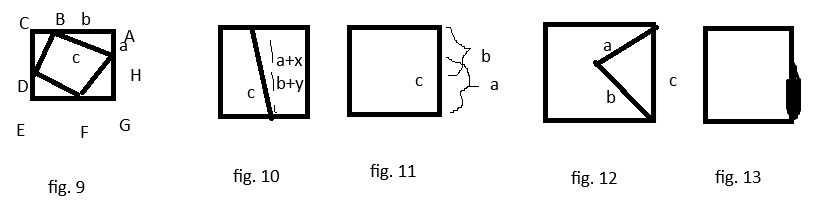
c will fit in the square because a and b fit in the square (fig. 5). WLOG (without loss of generality) c can connect edges. We can connect adjacent edges like fig. 6, have an edge like fig. 7, connect opposite edges like fig. 8, or have part of an edge like fig. 13. In the case of figure 6 we can have those edges be a and b. Usually the edges c connects make a and b to the point of c (like triangle ABH in figure 9).
For fig. 6, we can try 2 techniques in the next 2 paragraphs. I am confident the second one works, but I don’t want to erase the first.
In fig. 6 we want each triangle to have lengths a and b and to be the same size so it stretches around perfectly. See fig. 9. BH will have slope -a/b and BD b/a so they are perpendicular. They are also congruent. BC, DE and FG are a and CD, EF and GH are b. This will create c2 as the middle square and c2< the total square area (because there’s space left over), so we will be able to check if c2 < a2 + b2 is possible. BC will be y because AC is b+y and AB is b. Likewise GH will be x so that CD will be x. So BC= a and y and CD = b and x. Note that x2 < b2 (because b2 = ax+ax+x2 ) and y2 < a2 (because a2 = by+by+y2) so that x2+y2 < a2+b2 but they are also equal (because BC = a and y and CD = b and x like we mentioned two lines up). a2+b2 < a2 + b2, a contradiction. Then c2 is not less than a2+b2.
The second technique also involves fig. 6. c will form a square in the square, and we can allow the larger square to be a2+b2 by having the sides be a+x and b+y. Then we can test c2<a2+b2. Because the c square is symmetric, all sides are a and b together as well. Hence b=x and a=y. We have the same contradiction since x2 < b2 (because b2 = ax+ax+x2 ) and y2 < a2 (because a2 = by+by+y2) so that x2+y2 < a2+b2 but they are also equal. This shows that we cannot have c2<a2+b2.
Next we try fig. 10. This time it stretches past the length of an edge of the big square. One side will be a+x and b+y, so it will be bigger than a and bigger than b. That means we don’t have to consider it since it cannot be a and b.
Then c2 is not greater than a2+b2.
We don’t normally have to worry about bending c so that it’s in a different category or different; all cs will be tried.
The only thing left is that c is a side or partial side of the big square or parallel to it.
In fig. 13 c is a part of a side of the square. If c < a+x it could be less than a or b. Or importantly we can show that it won’t fit going across (adjacent sides) with the same a and b as normal legs. c might not match and a and b but it has to but it doesn’t but we don’t know that, so we apply the same argument with fig. 9. c2 will be given as < a2+b2 because that is the whole square and c has a length less than it’s side (c < a+x and a2+b2 we should know is (a+x)2 see fig. 1 and fig. 2).
All that’s left is c = a+x = b+y, one complete side. c2 = a2+b2 or if we look at (a+x)2 and (b+y)2 together we also get 2c2 = 2a2+2b2 (c2 = ax+ax+x2+a2 = a2+b2 and c2 = by+by+y2+b2 = a2+b2). It will look like figs. 11 and 12. Note that in fig. 12 it won’t be the same as like fig. 9 (it won’t stretch around evenly).